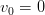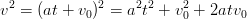Problème

Problème de physique simple: comment calculer la vitesse finale d'un objet, en chute libre d'une hauteur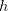 , sachant que la vitesse initiale est nulle, en supposant l'absence de frottements ?

Méthode 1: mouvement rectiligne uniformément accéléré

On a (formules générales MRUA)

1. 
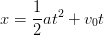
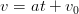2. (obtenu par dérivée de t de la formule précédente)

Or:

• 
• 
• 

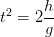donc, en 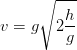substituant t de la première équation dans la 2e: ou encore (ou )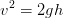

Rappelons que c'est un résultat important que la vitesse d'un corps en chute libre dans le vide (pas de frottement) ne dépend pas de sa masse mais de l'accélération (et de la hauteur). En pratique, les frottements de l'air vont faire se stabiliser la vitesse en fonction de la forme de l'objet.

Méthode 2: notion d'énergie et de travail

Le travail effectué dépend de la force et de la distance: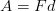 . La force est définie comme 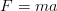. Donc ici 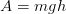. Comme l'énergie est définie comme 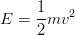, ou encore 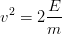et que l'on suppose que l'énergie potentielle a été réalisée dans le travail déplacement, on peut déduire que on encore que .

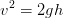Et si la vitesse initiale n'est pas nulle ?

En réfléchissant par énergie: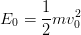 , d'où 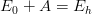, et donc 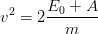, soit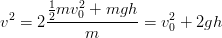

Et avec les équations MRUA:

1. 
2. 

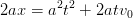en multipliant la 1ère équation par 2a: , on remarque la similitude avec la 2e et donc: .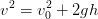

Administratif

• Set LATEXSCALEFACTOR = 1.0

-- MarcSCHAEFER - 13 Mar 2011